Transformimi i Furierit

Në matematikë, transformimi i Furierit është një metodë që transformon një sinjal në një varg numerik që tregon frekuencat e pranishme në sinjal. Funksioni i ri, i cili është paraqitja e funksionit në fushën e frekuencave të funksionit origjinal, tregon se cila nga frekuencat janë të pranishme në funksionin origjinal. Një analogji e vlefshme është rasti kur njerëzit mund të dëgjojnë se cilat nota luhen kur një violinist luan instrumentin. Pra në thelb, transformimi i Furierit bën dekompozimin e një funksioni në funksione sinusoidale dhe tregon se cila nga këto frekuenca të këtyre sinjaleve është e pranishme në sinjalin që po analizohet.Transformimi i Furierit është shumë i ngjashëm me transformime të tjera në matematikë të cilat së bashku formojnë degën e analizës se Furierit. Në ketë rast specifik, fushat e përcaktimit të funksionit origjinal dhe paraqitja në fushën e frekuencave janë kontinuume të vazhdueshme dhe të pa kufizuara. Termi transformimi i Furierit i referohet paraqitjes së funksionit në fushën e frekuencave ose operatorit/formulës që "transformon" një funksion në një tjetër.

E shprehur më formalisht, transformimi i Furierit transformon një funksion me vlerë komplekse të një ndryshoreje reale në një funksion tjetër. Transformimi i Furierit është një nga teknikat themelore të analizës së Furierit. Kjo teknikë mund të zgjerohet në mënyrë që të përfshijë shumë dimensione. Kjo gjen aplikime direkte në analizimin e imazheve. Aplikimi i transformimit të Furierit tek sinjalet digjitale,çoi në zbulimin e një metode tepër të shpejtë për llogaritjen e tij, e njohur si transformimi i shpejtë i Furierit.

Përcaktimi

Ka disa konvencione të ndryshme për përcaktimin e transformimit të Furierit të një funksioni të integrueshëm $f:R\to ℂ$ . Ky artikull përdor përcaktimin :

$\hat{f}(\xi ):=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)e^{-2\pi ix\xi }dx,$   per cdo numër real ξ.

Kur ndryshorja e pavarur $x$ paraqet kohën (me njësi SI në sekonda), ndryshorja e transformimit $\xi$ paraqet frekuencën (në herc). Në raste të favorshme, $f$ mund te rindërtohet $\hat{f}$ nga transformimi i anasjelltë:

$f(x)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\hat{f}(\xi )e^{2\pi ix\xi }d\xi ,$   për çdo numer real x.

Për konvencione të tjera të përdorura shikoni seksionet më poshtë.

Paraqitje e përgjithshme

Në studimin e serive të Furierit funksione të komplikuara shkruhen si shuma e funksioneve të thjeshta sinusoidale dhe kosinusoidale. Vetitë e këtyre funksioneve elementare bëjnë të mundur që të shprehim "sasinë" e këtye valëve në funksionin aktual përmes një integrali. Në shumë raste është e dëshirueshme që të përdorim formulën e Ojlerit, e cila pohon se $e^{2\pi \theta i}=\cos (2\pi \theta )+i\sin (2\pi \theta )$, në mënyrë që ti shkrujamë seritë e Furierit në terma të këtyre valëve elementare $e^{2\pi \theta i}$. Seritë e Furierit mund të përdoren për të arritur tek transformimi i Furierit në mënyrën e mëposhtme. Supozoni se $f$ është një funksion i cili është zero jashtë një intervali të caktuar $[-L/2,L/2]$. Atëherë për çdo $T\ge L$ mund ta zgjerojmë ƒ në një seri Furieri në intervalin $[-T/2,T/2]$, ku "shuma" (e dhene nga $c_n$) e valës $e^{2\pi inx/T}$ në serinë e Furierit të $f$ jepet nga

$\hat{f}(n/T)=c_n=\underset{-T/2}{\overset{T/2}{\int }}{e}^{-2\pi inx/T}f(x)dx$

dhe $f$ duhet të jepet nga formula

$f(x)=\frac{1}{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\hat{f}(n/T)e^{2\pi inx/T}.$

Po të lëmë ${\xi }_n=n/T$, dhe të lemë $\mathrm{\Delta }\xi =(n+1)/T-n/T=1/T$, atëhere kjo shuma e fundit kthehet ne një shumë Rimaniane

$f(x)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\hat{f}(n/T)e^{2\pi ix{\xi }_n}\mathrm{\Delta }\xi .$

Duke lënë $T\to -\mathrm{\infty }$ shuma e Rimanit konvergon tek integrali i transformimit të anasjelltë të Furierit i dhënë tek seksioni i përcaktimit. Nën situata të caktuara ky argument jepet në mënyrë preçize. Pra si në rastin e serive te Furierit, transformimi i Furierit mund të mendohet si një funksion që mat sa shumë prej cdo frekuence individuale është e pranishme tek funksioni jonë, rikombinimi i këtyre valëve duke përdorur një integral riprodhon funksionin origjinal.

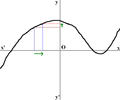
Figurat e mëposhtme japin një ilustrim sesi transformimi i Furierit matet nëqoftëse frekuenca është e pranishme në një funksion të caktuar. Funksioni i paraqitur $f(t)=\cos (6\pi t)e^{-\pi t^2}$ oshilon me 3 herc (nqs t matet në sekonda) dhe arrin shumë shpejt tek vlera 0. Ky funksion është zgjedhur specifikisht që të ketë një transformim real të Furierit i cili mund të vizatohet. Figura e parë përmban grafin e funksionit. Në mënyrë që të llogarisim $\hat{f}(3)$ +duhet të integrojmë $e^{-2\pi i(3t)}f(t),$ Figura e dytë tregon grafet e pjesëve reale dhe imagjinare të funksionit. Pjesa reale e integrantit është pothuajse gjithmonë pozitive, kjo ndodh sepse kur $f$ është negative $e^{-2\pi i(3t)}$ është negative gjithashtu. Meqenëse ato oshilojnë me të njëjtën shpejtësi kur ƒ është pozitive, ashtu eshtë edhe $e^{-2\pi i(3t)}$. Rezultati është që kur behet integrimi i pjesës reale te integrandit merret një numër relativisht i madh (0.5 në këtë rast). Nga ana tjetër, kur përpiqemi të matim një frekuencë $q$ nuk është e pranishme, si në rastin kur shikojmë $\hat{f}(5)$, integranti oshilon në mënyrë që vlera e integralit të jete shumë e vogël. Situata e përgjithshme është pak më e komplikuar, por në përgjithësi ky shembull tregon mënyrën se si transformimi i Furierit mat prezencën e një frekuence të caktuar në një funksion $f(t)$.

• 
  Funksioni origjinal tergon një oshilim me 3 herc.
• 
  Pjesa reale dhe imagjinare e integrantit te transformimit të Furierit në 3 herc
• 
  Pjesa reale dhe imagjinare e integrantit te transformimit të Furierit në 5 herc

Vetitë e transformimit të Furierit

Vetitë themelore

Le të marrim funksionet e integrueshme $f(x)$, $g(x)$, dhe $h(x)$ , gjithashtu le të quajmë transformimet e Furierit të tyre me $\hat{f}(\xi )$, $\hat{g}(\xi )$, dhe $\hat{h}(\xi )$ respektivisht. Transformimi i Furierit ka vetitë e mëposhtme themelore Stampa:Harv.

Lineariteti

për çdo numër kompleks a dhe b, nëqoftëse $h(x)=af(x)+bg(x)$, atëherë $\hat{h}(\xi )=a\cdot \hat{f}(\xi )+b\cdot \hat{g}(\xi ).$

Zhvendosja

Për çdo numër real $x_0$, nëqoftëse $h(x)=f(x-x_0)$ atëherë $\hat{h}(\xi )=e^{-2\pi i{x}_0\xi }\hat{f}(\xi ).$

Modulimi

Për çdo numër real ${\xi }_0$, nëqoftëse $h(x)=e^{2\pi ix{\xi }_0}f(x)$, atëherë  $\hat{h}(\xi )=\hat{f}(\xi -{\xi }_0)$.

Përshkallimi

Për çdo numër real jo-zero $a$, nëqoftëse $h(x)=f(ax)$, atëherë  $\hat{h}(\xi )=\frac{1}{|a|}\hat{f}\left(\frac{\xi }{a}\right)$.     Për rastin $a=-1$ kjo çon tek vetia e rikthimit-kohor, e cila pohon se: nëqoftëse $h(x)=f(-x)$, atëherë  $\hat{h}(\xi )=\hat{f}(-\xi )$.

Konjugimi

Nëqoftëse $h(x)=\overline{f(x)}$, atëherë  $\hat{h}(\xi )=\overline{\hat{f}(-\xi )}.$

Ne veçanti, nëqoftëse ƒ është reale, atëherë kemi konditën reale  $\hat{f}(-\xi )=\overline{\hat{f}(\xi )}.$

Dhe nëqoftëse ƒ numri është imagjinar, atëhere  $\hat{f}(-\xi )=-\overline{\hat{f}(\xi )}.$

Konvulimi

Nëqoftëse $h(x)=(f*g)(x)$, atëhere   $\hat{h}(\xi )=\hat{f}(\xi )\cdot \hat{g}(\xi ).$

Teorema e Plansharelit dhe teorema e Parsevalit

Le të jenë $f(x)$ dhe $g(x)$ funskione të integrueshme, dhe le të jenë $\hat{f}(\xi )$ dhe $\hat{g}(\xi )$ transformimet e tyre të Furierit. Nqs $f(x)$ dhe $g(x)$ janë të integrueshme në katror, atëhere kemi Teoremën e Parsevalit Stampa:Harv:

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)\overline{g(x)}dx=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\hat{f}(\xi )\overline{\hat{g}(\xi )}d\xi ,$

ku viza mbi tregon konjugimin kompleks.

Teorema e Plansharelit, e cila është ekuivalente me teoremën e Parsevalit, pohon se Stampa:Harv:

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{|f(x)|}^{2}dx=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{|\hat{f}(\xi )|}^{2}d\xi .$

Teorema e Plansharelit bën të mundur të përcaktojmë transformimin e Furierit për funksione në $L^2(𝑹)$, siç përshkruhet tek përgjithësimet më poshtë. Teorema e Plansharelit pohon se trasformimi i Furierit ruan energjinë e madhësisë origjinale të transformuar. Duhet të theksohet se në varësi të autorit këto teorema mund ti gjeni të referuara si teorema e Plansharelit ose si ajo e Parsevalit.

Shikoni artikullin mbi dualitetin e Pontryaginit për një formulim të përgjithshëm të këtij koncepti në kontekstin e grupeve lokale kompakte abeliane.

Formula e mbledhjes e Puasonit

Formula e mbledhjes e Puasonit jep një lidhje midis transformimit të Furierit dhe serive të Furierit. Po të kemi një funksion të integrueshëm $f$ mund të konsiderojmë periodizimin e $f$ të dhënë nga :

$\overline{f}(x)=\sum _{k\in \mathbb{Z}}f(x+k),$

ku shuma merret mbi të gjithë bashkësine e numrave të plote k. Formula e mbledhjes e Puasonit lidh seritë e Furierit me $\overline{f}$ transformimin e Furierit të $f$. Specifikisht ajo pohon se seritë e Furierit të $\overline{f}$ janë të dhëna nga:

$\overline{f}(x)\sim \sum _{k\in \mathbb{Z}}\hat{f}(k)e^{2\pi ikx}.$

Transformimi i Furierit në hapësirën Euklidiane

Transformimi i Furierit mund të ekzistojë në çdo numër arbitrar dimensionesh $n$. Ashtu si në rastin një dimensional ka shumë konvencione, për një funksion të integrueshëm $f(x)$ ky artikull adapton përkufizim:

$\hat{f}(\xi )=ℱ(f)(\xi )=\underset{{ℝ}^n}{\int }f(x)e^{-2\pi ix\cdot \xi }dx$

ku $x$ dhe $\xi$ jane vektorë n-përmasorë, dhe $x\bullet \xi$ është prodhimi i brendshëm i vektorëve. Prodhimi i brendshëm shkruhet ndonjëherë si $⟨x,\xi ⟩$.

Të gjitha të vetite bazë të përmendur më sipër jane te vlefshme për transformimin e Furierit n-permasor, e njejta gje mund te thuhet per teoremen e Plansharelit dhe teoremen e Parsevalit. Kur funksioni është i integrueshem, transformimi i Furierit eshte i vazhdueshëm dhe ende uniform lema Riemann-Lebesgue mban. Stampa:Harv

Parim i papërcaktueshmërisë

Në përgjithësi, sa më i përqëndruar te jete $f(x)$, aq më e përhapur është transformimi i Furierit $\hat{f}(\xi )$ . Në veçanti, vetia e shkallëzimit të transformimit të Furierit mund të shihet si më poshtë: nëse ne "shtrydh" një funksion në përmasën $x$, transformimi i Furierit tij "zgjerohet" në $\xi$. Nuk është e mundur që të përqëndrohemi në mënyrë arbitrare si tek një funksion ashtu edhe tek transformimi i Furierit i tij.

Shkëmbimi midis kompaktifikimit te nje funksionit dhe transformimi te Furierit te tij mund të formalizohet në formën e një parimi te papërcaktueshmërisë', dhe formalizohet duke e shikuar një funksion dhe transformimin e Furierit te tij si variabla te konjuguara në lidhje me formen simplektike në fushën kohë-frekuencë: nga pikëpamja e transformimeve lineare kanonike, transformimi i Furierit eshte nje rotullim me 90 ° ne fushen kohe-frekuencë, dhe si e tillë ruan formën simplektike.

Supozoni se funksion $f(x)$ është i integrueshem dhe i integrueshem ne katror. Pa humbje te përgjithshme, supozojmë se $f(x)$ është i normalizuar:

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|f(x){|}^{2}dx=1.$

Nga teorema e Plansherelit del që $\hat{f}(\xi )$  është e normalizuar gjithashtu.

Zgjerimi rreth x = 0, mund të matet me dispersionin rreth zero Stampa:Harv përcaktuar nga

$D_0(f)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{x}^2|f(x){|}^{2}dx.$

Në terma probabiliteti, kjo është momenti i dytë i $|f(x){|}^2$ rreth zero.

Parimi i papërcaktueshmërisë thekson se, në qoftë se $f(x)$ është absolutisht i vazhdueshëm dhe funksionet $x\cdot f(x)$ dhe $f^{\prime }(x)$ janë te integrueshme ne katror, atëherë

$D_0(f)D_0(\hat{f})\ge \frac{1}{16{\pi }^2}$    Stampa:Harv.

Barazisë është arritur vetëm në rastin $f(x)=C_1{e}^{-\pi x^2/{\sigma }^2}$    (hence   $\hat{f}(\xi )=\sigma C_1{e}^{-\pi {\sigma }^2{\xi }^2}$  )  , ku $\sigma >0$ është arbitrare dhe $C_1$ është e tillë që $f$ është $L^2$ - e normalizuar Stampa:Harv Me fjalë të tjera, ku $f$ është një funksion Gaussian i (normalizuar) , i përqendruar në zero.

Në fakt, kjo pabarazi nënkupton se:

$(\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(x-x_0{)}^2|f(x){|}^{2}dx)(\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(\xi -{\xi }_0{)}^2|\hat{f}(\xi ){|}^{2}d\xi )\ge \frac{1}{16{\pi }^2}$

për çdo $x_0,{\xi }_0$  në R  Stampa:Harv.

Në mekanikën kuantike, funksionet valore te momentit dhe pozicionit janë transformimet Furieri çifte, brenda një faktor të konstantes se Planckut. Me këtë konstante të marrë në konsideratë siç duhet, pabarazia më lart bëhet teorema e parimit të papërcaktueshmërisë e Heisenbergut (Stampa:Harv.

Alternativat

Në terminologjinë e përpunimit të sinjaleve , një funksion (kohor) është një përfaqësim i një sinjali me rezolucion të përsosur kohor,por pa informacion të frekuencave, ndërsa transformimi i Furierit ka rezolucion të përkryer të frekuencave, por nuk ka informacion kohor: madhësia e transformimit te Furierit në një pikë është se sa shumë përmbajtje frekuencash ka, por pozicioni është i dhënë vetëm nga faza (argumenti i transformimit te Furierit në një pikë), dhe valët qendruese nuk janë të lokalizuara në kohë - një valë sinusoidale vazhdon në pafundësi, pa u zvogëluar ne amplitude. Kjo kufizon dobine e transformimit te Furierit për të analizuar sinjalet që janë të lokalizuar në kohë, sidomos tranzientet, apo ndonjë sinjal me interval të fundëm.

Si alternativa të transformimit te Furierit , në analizën kohore të frekuencave, përdoren transformime kohë-frekuencë për të përfaqësuar sinjale në një formë që ka disa të dhëna në fushën kohore dhe disa informacione të frekuencave - nga parimi i papërcaktueshmersie. Këto transformime janë përgjithësimet te transformimit te Furierit , të tilla si transformimi i Furierit në kohë të shkurtër ose transformimi fraksional i Furierit , ose mund të përdorni funksione të ndryshme për të përfaqësuar sinjale, si valëzat dhe shndërrimet çirplet, për valëzat analogja me transformimin e (vazhdueshëm) të Furierit është transformimi i vazhdueshëm i valëzave.

Konvencione te tjera

Ekzistojne tre konvencione te zakonshme per percaktimin e transformimit te Furierit. Transformimi i Furierit zakonisht shkruhet ne terma te frekuencës këndore:   $\omega =2\pi \xi$ njesite e se ciles jane radian per sekonda.

Zevendesimi $\xi =\omega /(2\pi )$ ne formulen me lart jep konvencionin :

$\hat{f}(\omega )=\underset{{ℝ}^n}{\int }f(x)e^{-i\omega \cdot x}dx$

Nen kete konvencion, transformimi i anasjelltë bëhet:

$f(x)=\frac{1}{(2\pi {)}^n}\underset{{ℝ}^n}{\int }\hat{f}(\omega )e^{i\omega \cdot x}d\omega .$

Ne ndryshim nga konvencioni i perdorur ne kete artikull , kur transformimi i Furierit percaktohet ne kete menyre nuk eshte me e mundur te paraqitet si nje transformim unitar në $L^2({𝑹}^n)$. Gjithashtu ka me pak simetri midis formules se transformimit dhe inversit te saj.

Nje sistem tjeter percaktimi eshte kur ndajme faktorin $(2\pi {)}^n$ ne menyre te njejte midis transformimit Thurje dhe të anasjelltit të tij , gje e cila jep percaktimin :

$\hat{f}(\omega )=\frac{1}{(2\pi {)}^{n/2}}\underset{{ℝ}^n}{\int }f(x)e^{-i\omega \cdot x}dx$

$f(x)=\frac{1}{(2\pi {)}^{n/2}}\underset{{ℝ}^n}{\int }\hat{f}(\omega )e^{i\omega \cdot x}d\omega .$

Nen kete konvencion transfomimi i Furierit eshte prape nje transformim unitar në $L^2({𝑹}^n)$. Kjo rikthen simetrine midis transformimit te Furierit dhe inversit te tija.

Nje permbledhje e formave popullore per transfomimin e Furierit

Frekuenca e zakonshme ξ (hertz)	Unitare	${\hat{f}}_1(\xi )\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\underset{{ℝ}^n}{\int }f(x)e^{-2\pi ix\cdot \xi }dx={\hat{f}}_2(2\pi \xi )=(2\pi {)}^{n/2}{\hat{f}}_3(2\pi \xi )$ $f(x)=\underset{{ℝ}^n}{\int }{\hat{f}}_1(\xi )e^{2\pi ix\cdot \xi }d\xi$
Frekuenca kendore $\omega$ (rad/s)	Jo-unitare	${\hat{f}}_2(\omega )\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\underset{{ℝ}^n}{\int }f(x)e^{-i\omega \cdot x}dx={\hat{f}}_1\left(\frac{\omega }{2\pi }\right)=(2\pi {)}^{n/2}{\hat{f}}_3(\omega )$ $f(x)=\frac{1}{(2\pi {)}^n}\underset{{ℝ}^n}{\int }{\hat{f}}_2(\omega )e^{i\omega \cdot x}d\omega$
	Unitare	${\hat{f}}_3(\omega )\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{(2\pi {)}^{n/2}}\underset{{ℝ}^n}{\int }f(x)e^{-i\omega \cdot x}dx=\frac{1}{(2\pi {)}^{n/2}}{\hat{f}}_1\left(\frac{\omega }{2\pi }\right)=\frac{1}{(2\pi {)}^{n/2}}{\hat{f}}_2(\omega )$ $f(x)=\frac{1}{(2\pi {)}^{n/2}}\underset{{ℝ}^n}{\int }{\hat{f}}_3(\omega )e^{i\omega \cdot x}d\omega$

Tabela me transformime te rendesishme te Furierit

Tabelat e meposhtme japin disa nga format e mbyllura te transformimit te Furierit. Per funksionet $f(x)$ , $g(x)$ dhe $h(x)$ transformimet e Furirit jane te dhena nga $\hat{f}$, $\hat{g}$, dhe $\hat{h}$ respektivisht. Vetem tre konvencionet me te zakonshme jane te perfshira.

Funksione, katrori i se cilave eshgte i integrueshem

	Funksioni	Transformimi i Furierit unitar, Frekuenca kendore	Transformimi i Furierit unitar, frekuenca e zakonshme	Transformimi i Furierit jo-unitar, Frekuenca kendore	Shenime
	$f(x)$	$\hat{f}(\xi )=$ $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)e^{-2\pi ix\xi }dx$	$\hat{f}(\omega )=$ $\frac{1}{\sqrt{2\pi }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)e^{-i\omega x}dx$	$\hat{f}(\nu )=$ $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(x)e^{-i\nu x}dx$
201	$\mathrm{rect}(ax)$	$\frac{1}{|a|}\cdot \mathrm{sinc}\left(\frac{\xi }{a}\right)$	$\frac{1}{\sqrt{2\pi a^2}}\cdot \mathrm{sinc}\left(\frac{\omega }{2\pi a}\right)$	$\frac{1}{|a|}\cdot \mathrm{sinc}\left(\frac{\nu }{2\pi a}\right)$	Pulsi rektangular dhe Funksioni sink i normalizuar, i percaktuar ketu si $\mathrm{sinc}(x)=\sin (\pi x)/(\pi x)$
202	$\mathrm{sinc}(ax)$	$\frac{1}{|a|}\cdot \mathrm{rect}\left(\frac{\xi }{a}\right)$	$\frac{1}{\sqrt{2\pi a^2}}\cdot \mathrm{rect}\left(\frac{\omega }{2\pi a}\right)$	$\frac{1}{|a|}\cdot \mathrm{rect}\left(\frac{\nu }{2\pi a}\right)$	Duali i rregullit 201. Funksioni drejtkendesh eshte nje filter i frekuencave te ulta, dhe funksioni sink eshte pergjigjja impulsive jokauzale e nje filteri te tille.
203	${\mathrm{sinc}}^2(ax)$	$\frac{1}{|a|}\cdot \mathrm{tri}\left(\frac{\xi }{a}\right)$	$\frac{1}{\sqrt{2\pi a^2}}\cdot \mathrm{tri}\left(\frac{\omega }{2\pi a}\right)$	$\frac{1}{|a|}\cdot \mathrm{tri}\left(\frac{\nu }{2\pi a}\right)$	Funksioni $\mathrm{tri}(x)$ eshte funksioni trekendesh
204	$\mathrm{tri}(ax)$	$\frac{1}{|a|}\cdot {\mathrm{sinc}}^2\left(\frac{\xi }{a}\right)$	$\frac{1}{\sqrt{2\pi a^2}}\cdot {\mathrm{sinc}}^2\left(\frac{\omega }{2\pi a}\right)$	$\frac{1}{|a|}\cdot {\mathrm{sinc}}^2\left(\frac{\nu }{2\pi a}\right)$	Ligji dual i rregullit 203.
205	$e^{-ax}u(x)$	$\frac{1}{a+2\pi i\xi }$	$\frac{1}{\sqrt{2\pi }(a+i\omega )}$	$\frac{1}{a+i\nu }$	Funksioni $u(x)$ eshte Funksioni shkalle Heaviside dhe a>0.
206	$e^{-\alpha x^2}$	$\sqrt{\frac{\pi }{\alpha }}\cdot e^{-\frac{(\pi \xi {)}^2}{\alpha }}$	$\frac{1}{\sqrt{2\alpha }}\cdot e^{-\frac{{\omega }^2}{4\alpha }}$	$\sqrt{\frac{\pi }{\alpha }}\cdot e^{-\frac{{\nu }^2}{4\alpha }}$	Kjo tregon se , per transfromimet unitare te Furierit, Funksioni Gausian $e^{-\alpha x^2}$ eshte transformimi i Furierit i vetvetes per nje zgjedhje te α. Per kete qe te jete e integrueshme duhet te kemi $\mathrm{Re}(\alpha )>0$.
207	${\mathrm{e}}^{-a|x|}$	$\frac{2a}{a^2+4{\pi }^2{\xi }^2}$	$\sqrt{\frac{2}{\pi }}\cdot \frac{a}{a^2+{\omega }^2}$	$\frac{2a}{a^2+{\nu }^2}$	Per a>0.
208	$\frac{J_n(x)}{x}$	$\frac{2i}{n}(-i{)}^n\cdot U_{n-1}(2\pi \xi )$   $\cdot \sqrt{1-4{\pi }^2{\xi }^2}\mathrm{rect}(\pi \xi )$	$\sqrt{\frac{2}{\pi }}\frac{i}{n}(-i{)}^n\cdot U_{n-1}(\omega )$   $\cdot \sqrt{1-{\omega }^2}\mathrm{rect}\left(\frac{\omega }{2}\right)$	$\frac{2i}{n}(-i{)}^n\cdot U_{n-1}(\nu )$   $\cdot \sqrt{1-{\nu }^2}\mathrm{rect}\left(\frac{\nu }{2}\right)$	Funksionet $J_n(x)$ janë funksionet e Beselit të rendit n të llojit të parë. Funksionet $U_n(x)$ jane Polinomet e Çebishevit te rendit te dyte. Shiko 315 dhe 316 poshte.
209	$\mathrm{sech}(ax)$	$\frac{\pi }{a}\mathrm{sech}\left(\frac{{\pi }^2}{a}\xi \right)$	$\frac{1}{a}\sqrt{\frac{\pi }{2}}\mathrm{sech}\left(\frac{\pi }{2a}\omega \right)$	$\frac{\pi }{a}\mathrm{sech}\left(\frac{\pi }{2a}\nu \right)$	Sekanti hiperbolik eshte transformimi i Furierit i vetvetes

Shih edhe

• Transformimi i Furierit në kohë diskrete

Lidhje te jashtme

• Всё о Mathcad Stampa:Webarchive Stampa:Ref-ru
• Fourier Series Applet (Tip: drag magnitude or phase dots up or down to change the wave form).
• Tables of Integral Transforms at EqWorld: The World of Mathematical Equations.
• Stampa:MathWorld
• Fourier Transform Module by John H. Mathews
• The DFT “à Pied”: Mastering The Fourier Transform in One Day at The DSP Dimension